Pond-Free 102 Chapter 2
Water Matrix Reservoirs
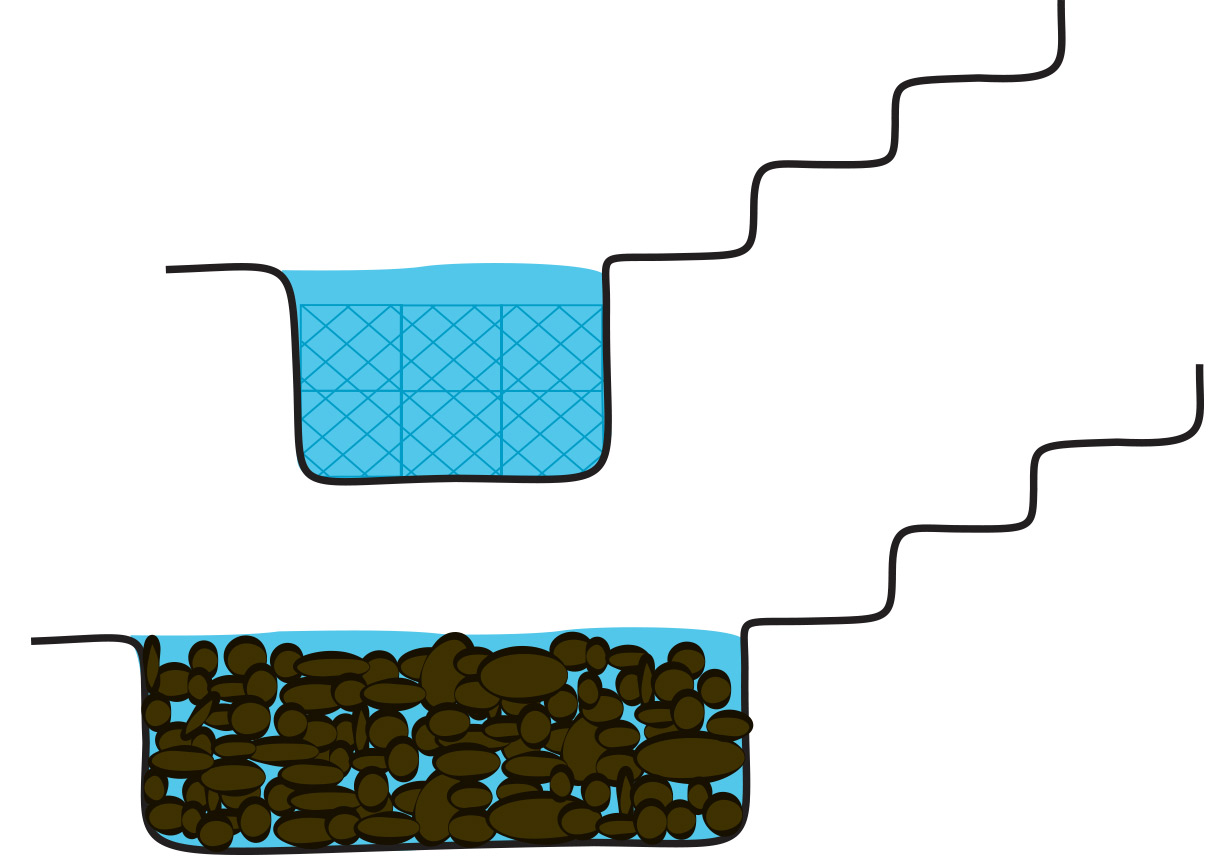
It’s easy to say that reservoirs made with Water Matrices are ‘better’ than gravel-filled reservoirs, but it’s more useful to do the math. Let's say for the sake of argument that you want to build about 9´ total of stream and waterfalls and you want to compare the size and cost of a Graveled Reservoir versus one made with Water Matrices. Let's guesstimate that, in our hypothetical illustration, the 8' long stream varies in width from 1´ to 4´ wide, but the average width of the stream and falls is about 2´ wide; we'll guess that the average depth we have to fill including every pocket and pool is a modest 3˝ before the water flows back into the gravel. If we calculate the volume of water we'll need in the stream and falls to get the feature running at 8´ long by 2´ wide by 3˝ (1/4 foot), we'll need about 1/4 of 16, or 4 cubic feet of Dynamic Volume. We’ll want to drop the water level in the reservoir by only a third, so we’ll need 12 cubic feet in the reservoir in order to maintain at least eight cubic feet around and over the pump when it’s running. To have enough room for 1/3 water and 2/3 gravel besides, we’ll need at least three times the Total Volume, or nine times the Dynamic Volume, for our graveled reservoir, 36 cubic feet to hold the 12 cubic feet of water, so the water will only drop by a third in the reservoir on startup. That’s a hole 3 feet deep by 3 wide by 4 long, plus 1¼ cubic yards of gravel weighing one and a half TONS. That’s a good half-day’s work for three men by hand in soft soil, and it’s not much less even with a machine when you consider cleaning up after a skid steer or mini-excavator.
Using Water Matrices, we can store the same volume of water, 12 cubic feet, in a 12 cubic foot reservoir. There’s one-third as much digging required, for a hole only 2 foot deep by 2 wide by 3 long; and installing 3 matrices will take a tiny fraction of the time and effort required to backfill with 3000 lbs. of gravel. Now, 3 matrices will usually cost more than a ton and a half of gravel, but the savings in time, effort and cleanup more than makes up the difference. In fact, instead of the minimum 9 times the Dynamic Volume for graveled reservoirs, you will only need one third as much: 3 times the Dynamic Volume for your matrix reservoir. That’s a big difference.

It’s easy to say that reservoirs made with Water Matrices are ‘better’ than gravel-filled reservoirs, but it’s more useful to do the math. Let's say for the sake of argument that you want to build about 9´ total of stream and waterfalls and you want to compare the size and cost of a Graveled Reservoir versus one made with Water Matrices. Let's guesstimate that, in our hypothetical illustration, the 8' long stream varies in width from 1´ to 4´ wide, but the average width of the stream and falls is about 2´ wide; we'll guess that the average depth we have to fill including every pocket and pool is a modest 3˝ before the water flows back into the gravel. If we calculate the volume of water we'll need in the stream and falls to get the feature running at 8´ long by 2´ wide by 3˝ (1/4 foot), we'll need about 1/4 of 16, or 4 cubic feet of Dynamic Volume. We’ll want to drop the water level in the reservoir by only a third, so we’ll need 12 cubic feet in the reservoir in order to maintain at least eight cubic feet around and over the pump when it’s running. To have enough room for 1/3 water and 2/3 gravel besides, we’ll need at least three times the Total Volume, or nine times the Dynamic Volume, for our graveled reservoir, 36 cubic feet to hold the 12 cubic feet of water, so the water will only drop by a third in the reservoir on startup. That’s a hole 3 feet deep by 3 wide by 4 long, plus 1¼ cubic yards of gravel weighing one and a half TONS. That’s a good half-day’s work for three men by hand in soft soil, and it’s not much less even with a machine when you consider cleaning up after a skid steer or mini-excavator.
Using Water Matrices, we can store the same volume of water, 12 cubic feet, in a 12 cubic foot reservoir. There’s one-third as much digging required, for a hole only 2 foot deep by 2 wide by 3 long; and installing 3 matrices will take a tiny fraction of the time and effort required to backfill with 3000 lbs. of gravel. Now, 3 matrices will usually cost more than a ton and a half of gravel, but the savings in time, effort and cleanup more than makes up the difference. In fact, instead of the minimum 9 times the Dynamic Volume for graveled reservoirs, you will only need one third as much: 3 times the Dynamic Volume for your matrix reservoir. That’s a big difference.




